Basic usage • twigstats

The main use-case of Twigstats is to compute f2-statistics for pairs of populations.

This should be straight forward: We compute these using a single function call in R, using the output files of Relate as input. The output can then directly be fed into functions of the admixtools2 R package (https://uqrmaie1.github.io/admixtools/index.html) to compute any other f-statistic.

Each function implemented in the Twigstats package is described on this page: leospeidel.com/twigstats/reference.

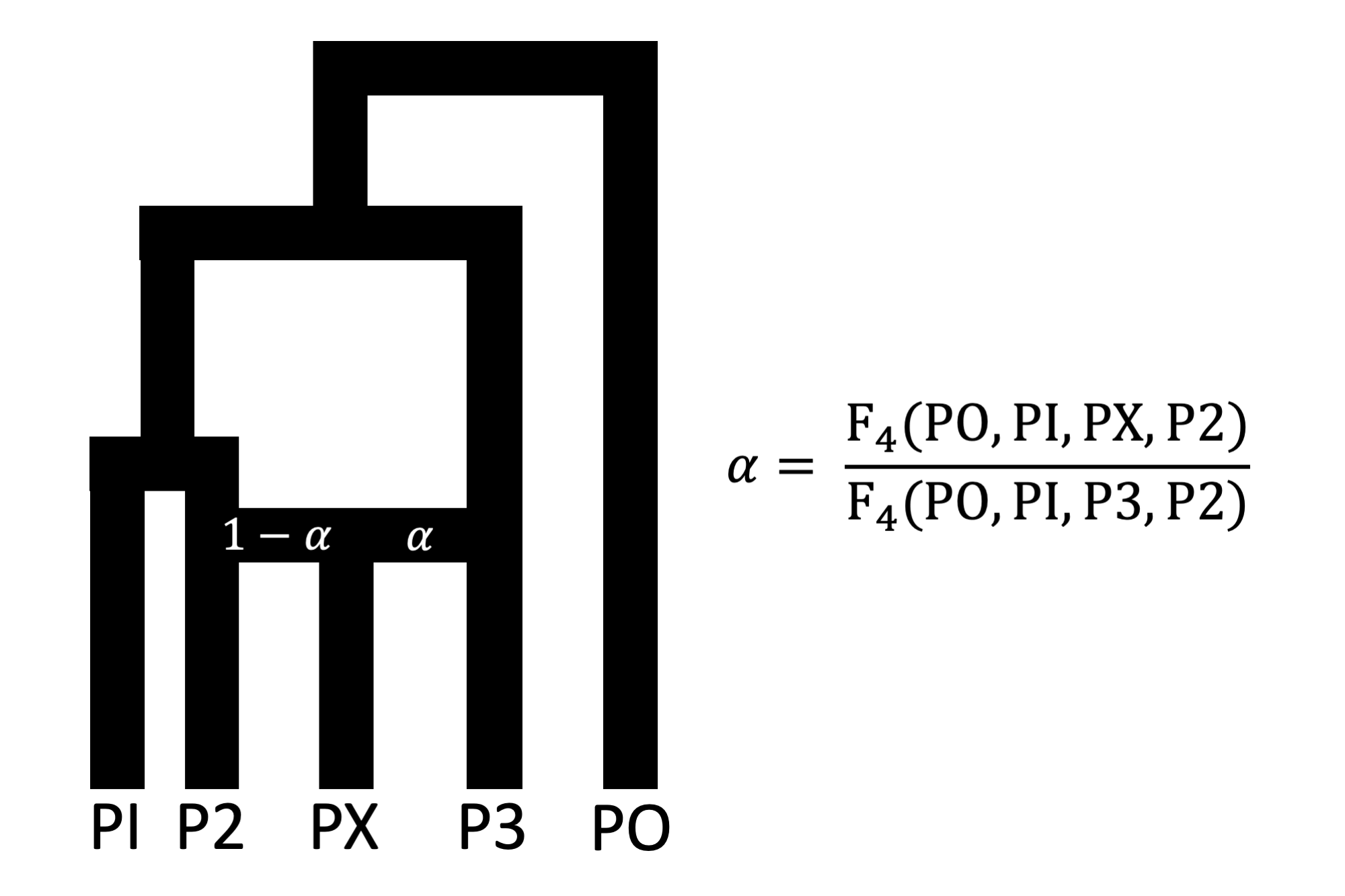
Here, we will demonstrate key features using an example stored under inst/sim/, which contains simulated data for five populations as described in our paper (Figure 1).

library(twigstats)
#> Loading required package: dplyr
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union

Computing f2-statistics from Relate genealogies

The first use-case is to compute f2-statistics on Relate genealogies (https://myersgroup.github.io/relate/).

The central function is called f2_blocks_from_Relate() which takes Relate output files as input.
Please type ?f2_blocks_from_Relate for more details:

We will illustrate a basic Twigstats run using example files that are included in the Twigstats package. In this example, population PX is admixed between populations P2 and P3, with a mixture proportion of 20% and 80%, respectively.

These lines assign filenames to variables file_anc, file_mut, poplabels, and file_map.

#see https://myersgroup.github.io/relate/getting_started.html#Output for file formats
file_anc  <- system.file("sim/msprime_ad0.8_split250_1_chr1.anc.gz", package = "twigstats")
file_mut  <- system.file("sim/msprime_ad0.8_split250_1_chr1.mut.gz", package = "twigstats")
#see https://myersgroup.github.io/relate/input_data.html for file formats
poplabels <- system.file("sim/msprime_ad0.8_split250_1.poplabels", package = "twigstats")
file_map  <- system.file("sim/genetic_map_combined_b37_chr1.txt", package = "twigstats") #recombination map (three column format)

We will first calculate f2 statistics as normal without a cutoff.
We will then plug these f2 statistics into an f4-ratio statistic which computes an estimate of the admixture proportion.

#Calculate regular f2s between all pairs of populations
f2_blocks1 <- f2_blocks_from_Relate(file_anc, file_mut, poplabels, file_map)
f4_ratio(f2_blocks1, popX="PX", popI="P1", pop1="P2", pop2="P3", popO="P4")
#>   popO popI pop1 pop2 popX       val        se
#> 1   P4   P1   P2   P3   PX 0.9974217 0.3076228

As we can see, the inferred admixture proportion is not close to the true value of 80% and the standard errors are large. This shows that we are underpowered to infer the admixture proportions using this f4-ratio statistic.

Now we will specify a twigstats cutoff of 500 generations and plug these into an f4-ratio statistic:

#Now calculate f2s using a twigstats cutoff of 500 generations. 
#This should give us a big power boost.
f2_blocks2 <- f2_blocks_from_Relate(file_anc, file_mut, poplabels, file_map, t = 500)
f4_ratio(f2_blocks2, popX="PX", popI="P1", pop1="P2", pop2="P3", popO="P4")
#>   popO popI pop1 pop2 popX       val         se
#> 1   P4   P1   P2   P3   PX 0.8110266 0.02085804

The standard errors are much reduced!

Use argument use_muts to compute f2-statistics on the (age-ascertained) mutations, instead of branch lengths of Relate genealogies.
Use argument blgsize to change jackknife block size
Set argument transitions to False to exclude transitions

Using admixtools2

We can now directly feed this into admixtools2 functions:

library(admixtools)
#no twigstats ascertainment
f4(f2_blocks1, "P4", "P3", "P2", "PX")
#> # A tibble: 1 × 8
#>   pop1  pop2  pop3  pop4      est       se     z         p
#>   <chr> <chr> <chr> <chr>   <dbl>    <dbl> <dbl>     <dbl>
#> 1 P4    P3    P2    PX    0.00127 0.000314  4.04 0.0000543
#with twigstats ascertainment
f4(f2_blocks2, "P4", "P3", "P2", "PX")
#> # A tibble: 1 × 8
#>   pop1  pop2  pop3  pop4       est        se     z         p
#>   <chr> <chr> <chr> <chr>    <dbl>     <dbl> <dbl>     <dbl>
#> 1 P4    P3    P2    PX    0.000635 0.0000253  25.1 1.37e-138

If PX exclusively clustered with P2 and did not carry gene flow from P3, we expect this f4 statistic to not be significantly deviating from 0. We observe a highly significant attraction of P3 to PX, especially when ascertaining coalescences of the last 500 generations using Twigstats, consistent with PX being a mixture of P2 and P3.

Computing f2-statistics on age-ascertained SNPs

Sometimes, we are prefer not to graft samples into genealogies (e.g. due to low sequencing coverage, or if we don’t trust the imputation).
Therefore, the second use-case of Twigstats is to compute f2-statistics on age ascertained mutations.

The central function is called f2_blocks_from_RelateAges() which takes plink (bed/bim/fam) files and mutation ages (.mut) as input.
Please type ?f2_blocks_from_RelateAges for more details:

We will begin with assigning filenames to the following variables. In our case, all files are stored under path and have prefix pref.

path <- paste0(system.file("sim/", package = "twigstats"),"/")
pref <- "msprime_ad0.8_split250_1"
file_plink <- paste0(path,pref) #only need prefix
file_mut  <- paste0(path,pref) #only need prefix (here same name as plink file but can be different)

Next, we compute f2-statistics as normal on the plink format and plug these into an f4-ratio statistic to estimate the admixture proportion.

#Compute regular f2 statistics between all pairs of populations. You can use pops to only calculate f2s between specified populations.
f2_blocks1 <- f2_blocks_from_RelateAges(pref = file_plink, file_mut)
f4_ratio(f2_blocks1, popX="PX", popI="P1", pop1="P2", pop2="P3", popO="P4")
#>   popO popI pop1 pop2 popX      val        se
#> 1   P4   P1   P2   P3   PX 1.082681 0.2931867

As before, we can see that the standard error of the inferred dmixture proportion is very large. This shows we are lacking power using the standard f-statistics approach.

We can now ascertain mutations by age. Here we choose a cutoff of 500 generations:

#Use a cutoff of 500 generations
f2_blocks2 <- f2_blocks_from_RelateAges(pref = file_plink, file_mut, t = 500)
f4_ratio(f2_blocks2, popX="PX", popI="P1", pop1="P2", pop2="P3", popO="P4")
#>   popO popI pop1 pop2 popX      val         se
#> 1   P4   P1   P2   P3   PX 0.810077 0.03097378

The standard errors are much reduced! So while we are unable to get a reliable estimate without twigstats ascertainment, we estimate PX to carry approximately 80% P2 and 20% P3 ancestry with twigstats.

Use argument pops to analyse a subset of populations and fam to change population assignment of individuals
Use argument blgsize to change jackknife block size
Set argument transitions to False to exclude transitions
Use file_mut = “./1240k/1240k” to calculate f2 statistics at 1240k sites
Use file_mut = “./1000G_ages/1000GP_Phase3_mask_prene_nosingle_chr1” to calculate f2 statistics at 1240k sites

Using admixtools2

We can now directly feed this into admixtools2 functions:

library(admixtools)
#no twigstats ascertainment
f4(f2_blocks1, "P4", "P3", "P2", "PX")
#> # A tibble: 1 × 8
#>   pop1  pop2  pop3  pop4      est       se     z        p
#>   <chr> <chr> <chr> <chr>   <dbl>    <dbl> <dbl>    <dbl>
#> 1 P4    P3    P2    PX    0.00116 0.000305  3.81 0.000139
#with twigstats ascertainment
f4(f2_blocks2, "P4", "P3", "P2", "PX")
#> # A tibble: 1 × 8
#>   pop1  pop2  pop3  pop4       est        se     z         p
#>   <chr> <chr> <chr> <chr>    <dbl>     <dbl> <dbl>     <dbl>
#> 1 P4    P3    P2    PX    0.000642 0.0000281  22.9 9.35e-116

As before, we find a highly significant attraction of P3 to PX using Twigstats, consistent with PX being a mixture of P2 and P3.